《数值计算方法》课设-迭代法在数值计算方法中的运用

请设置文章作者

发布于：2018年6月15日

摘要

迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程，跟迭代法相对应的是直接法(或者称为一次解法)，即一次性解决问题。迭代算法是用计算机解决问题的一种基本方法，它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令(或一定步骤)进行重复执行，在每次执行这组指令(或这些步骤)时，都从变量的原值推出它的一个新值，迭代法又分为精确迭代和近似迭代。比较典型的迭代法如“二分法”和”牛顿迭代法”属于近似迭代法。

在这篇文章里，主要介绍迭代法在线性方程组的数值解法和非线性方程组中迭代法运用，以及迭代法在数据结构算法中的优化和计算机视觉算法的运用。

关键词：

Jacobi 迭代法
Gauss-Seidel 迭代法
Newton-Raphson 迭代法

工具&语言：Matlab， C++

1. 迭代法在线性方程组数值解法中的运用

解线性方程组的迭代法是对任意给定的初始近似解向量，按着某种方法逐步生成近似解序列，使解序列的极限为方程的解。因此迭代是利用某种极限过程去逐步逼近精确解的方法，从而可以利用有限步计算算出指定精度的近似解。迭代法主要有：Jacobi 迭代法、Gauss-Seidel 迭代法和超松弛迭代法。

1.1 迭代法的一般形式

设有线性方程组

矩阵形式（1.1）：

$Ax = b$

分量形式（1.2）：
$\begin{cases} a_{11}x_1&+&a_{12}x_2&+&\cdots&+a_{1n}x_n&=&b_1\\ a_{21}x_1&+&a_{22}x_2&+&\cdots&+a_{2n}x_n&=&b_2\\ &&&&\vdots\\ a_{n1}x_1&+&a_{n2}x_2&+&\cdots&+a_{nn}x_n&=&b_n& \end{cases}$

以矩阵形式进行阐述，其中$A$为非奇异矩阵，向量$b\neq0$，因而有唯一解$x^\ast$。下面介绍迭代法的一般形式。

先将方程组变形为等价的同解线性方程组（1.3）

$x = Bx + f$

的形式，然后任取一个初始向量$x^{(0)}\epsilon R^n$作为近似解，由公式（1.4）

$x^{(k+1)}=Bx^{(k)}+f, \quad k=0,1,2,\cdots$

构造向量序列$\lbrace x^{(k)}\rbrace$，如果向量序列$\lbrace x^{(k)}\rbrace$满足（1.5）

$\lim_{k \to +\infty} x^{(k)} = x^\ast$

则称迭代法收敛，$x^\ast$即是方程组（1.2）的解，否则，称迭代法发散。式（1.4）称为迭代形式，$B$为迭代矩阵，$x^{(k)}$为第$k$次迭代近似解，称$e^{(k)} = x^{*} + x^{(k)}$为第k次迭代误差。

1.2 Jacobi迭代法及算法实现

Jacobi迭代法的分量形式
设线性方程（1.1）的分量形式为（1.6）
$\begin{cases} a_{11}x_1&+&a_{12}x_2&+&\cdots&+a_{1n}x_n&=&b_1\\ a_{21}x_1&+&a_{22}x_2&+&\cdots&+a_{2n}x_n&=&b_2\\ &&&&\vdots\\ a_{n1}x_1&+&a_{n2}x_2&+&\cdots&+a_{nn}x_n&=&b_n& \end{cases}$
Jacobi的迭代步骤：

（1）设$a{ii} \neq 0(i = 1,2,\cdots,n)$. 将线性方程组（1.6）的第$i$个方程中的第$i$个变元$x{i}$用其他$n-1$个变元表示，即解出（1.7）
$\begin{cases} x_1=\frac{1}{a_{11}}(b_1&-&a_{12}x_2&-&a_{13}x_3&-&\cdots&-&a_{1n}x_n)&\\ x_2=\frac{1}{a_{22}}(b_2&-&a_{21}x_1&-&a_{23}x_3&-&\cdots&-&a_{2n}x_n)&\\ &&&&\vdots\\ x_n=\frac{1}{a_{nn}}(b_n&-&a_{n1}x_1&-&a_{n2}x_2&-&\cdots&-&a_{n,n-1}x_{n-1})&\\ \end{cases}$
即（1.8）
$x_i=\frac{b_i - \sum_{j=1,j \neq i}^{n} a_{ij}x_j}{a_{ii}}, \quad i = 1,2,\cdots,n.$
(2)写成迭代形式（1.9）
$\begin{cases} x_1^{(k+1)}=\frac{1}{a_{11}}(b_1&-&a_{12}x_2^{(k)}&-&a_{13}x_3^{(k)}&-&\cdots&-&a_{1n}x_n^{(k)})&\\ x_2^{(k+1)}=\frac{1}{a_{22}}(b_2&-&a_{21}x_1^{(k)}&-&a_{23}x_3^{(k)}&-&\cdots&-&a_{2n}x_n^{(k)})&\\ &&&&\vdots\\ x_n^{(k+1)}=\frac{1}{a_{nn}}(b_n&-&a_{n1}x_1^{(k)}&-&a_{n2}x_2^{(k)}&-&\cdots&-&a_{n,n-1}x_{n-1}^{(k)})&\\ \end{cases}$
即（1.10）
$x_i^{(k+1)} = \frac{b_i - \sum_{j=1,j \neq i}^n a_{ij}x_j^{(k)}}{a_{ii}}, \quad i = 1,2,\cdots,n;k = 0,1,2,\cdots.$
(3)取初值向量$x^{(0)} = (x_1^{(0)},x_2^{(0)},\cdots,x_n^{(0)})^T$代入（1.9），逐次算出向量序列$\lbrace x^{(k)}\rbrace (K=1,2,\cdots)$，这里$x^{(k)} = (x_1^{(k)},x_2^{(k)},\cdots,x_n^{(k)})^T$. 向量序列$\lbrace x^{(k)}\rbrace$收敛时，对于事先给定的精度要求$\epsilon$, 当
$\mid\mid x^{(k+1}) - x^{(k)}\mid\mid_{\infty} < \epsilon$
时，即得方程组的近似解$x^{*}\approx x^{(k+1)}$.
Jacobi的矩阵形式

设线性方程组（1.1）的系数矩阵A非奇异，且主对角线元素$a_{ii}\neq 0(i=1,2,\cdots,n)$，将矩阵A分解为（1.11）
$A = \begin{pmatrix} 0 \\ a_{21} & 0 \\ \vdots & \vdots & \ddots \\ a_{n1} & a_{n2} & \cdots & 0 \\ \end{pmatrix} + \begin{pmatrix} a_{11} \\ & a_{22} \\ & & \ddots \\ & & & a_{nn} \\ \end{pmatrix} + \begin{pmatrix} 0 & a_{12} & \cdots & a_{1n} \\ & 0 & \cdots & a_{2n} \\ & & \ddots & \vdots \\ & & & 0 \\ \end{pmatrix}$
记作
$A = L + D + U$
则$Ax=b$等价于
$(L+D+U)x = b$
即
$Dx = -(L+U)x + b$
由$a_{ii}\neq 0(i=1,2,\cdots,n)$，则
$x = -D^{-1}(L+U)x + D^{-1}b$
得迭代格式（1.12）：
$x^{(K+1)} = -D^{-1}(L+U)x^{k} + D^{-1}b$
令
$B=-D^{-1}(L+U);f=D^{-1}b$
则有（1.13）
$x^{(k+1)}= Bx^{(k)}+f$
称式（1.13）为Jacobi迭代式得矩阵形式，其中$B$称为Jacobi迭代矩阵，Jacobi迭代法的矩阵形式，主要用来讨论其收敛性，实际计算中，常用分量形式。

Jacobi迭代法的MATLAB程序
(1). 分量形式

function [x,k] = jacobif(A,b,x0,ep,Nmax)
% 用分量形式jacobi迭代法解线性方程组Ax=b
% [x,k]=jacobif(A,b,x0,ep,Nmax),A为系数矩阵，b为右端向量，x为返回解向量
% x0为迭代初值（默认值为原点），ep为精度（默认值为1e-5）
% k为迭代次数上限以防法发散（默认值为500）
n=length(A);k=0;
if nargin<5 Nmax=500;end
if nargin<4 ep=1e-5;end
if nargin<3 x0=zeros(n,1);y=zeros(n,1);end
x=x0;x0=x+2*ep;
while norm(x0-x,inf)>ep&&k<Nmax,k=k+1;x0=x;
	for i=1:n
		y(i)=b(i);
		for j=1:n
			if j~=i
				y(i)=y(i)-A(i,j)*x0(j);
			end
		end
		if abs(A(i,i))<1e-10||k==Nmax
			warning('A(i,i) is small');
			return
		end
	y(i)=y(i)/A(i,i);
	end
	x=y;
end

（2）矩阵形式

% 雅可比迭代法，计算线性方程组的解
function  [x,k] = jacobi_iteration(A,b,x0,tol)
% tol为输入误差容限，x0为迭代初始值

% 默认最多迭代300次，超出300次会给出警示
max1 = 300;  

%求A的对角矩阵
D = diag(diag(A));

%求A的下三角矩阵
%% 虽然查MATLAB的文档里tril和triu没有什么区别，但是实际写代码的时候
%% 还是会有差别的，总之记住这应上三角和下三角的表示方法就好了
%%% 这里加负号的原因是由雅可比迭代的原理可知的，需要下三角矩阵的每个元素取负
%%% 下面的U也是同样的道理
L = -tril(A,-1);

%求A的上三角矩阵
U = -triu(A,1);

% \表示对D求逆之后乘以（L+U）和b
B = D\(L+U);
f = D\b;

x = B*x0+f;
k = 1;

% norm是取二范数的意思
while norm(x-x0)>=tol
	x0 = x;
	x = B*x0+f;
	k = k+1;
	if(k>=max1)
		% 输出内容的函数
		disp('迭代次数超过',max1,'次，方程组可能不收敛');
		
		%% 在MATLAB中遇到return的意思就是结束整个函数的执行，
		%% break是仅仅跳出循环体
		return;
	end
	
	%该命令的作用是显示每一步的迭代结果,注意x是列向量，’表示转置的意思，所以要加’
	[k,x']
end

jacobi迭代法的C++程序

//函数求数组中的最大值  
double MaxOfList(vector<double>x){  
	double max=x[0];  
	int n=x.size();  
	for(int i=0;i<n;i++)  
		if(x[i]>max) max=x[i];  
	return max;  
}  

//雅可比迭代公式  
void Jacobi(vector<vector<double> > A,vector<double> B,int n){  
	vector<double> X(n,0);  
	vector<double> Y(n,0);  
	vector<double> D(n,0);  
	int k=0; //记录循环次数  
	do{   
		X=Y;  
		for(int i=0;i<n;i++){  
			double tem=0;  
			for(int j=0;j<n;j++){  
				if(i!=j) tem += A[i][j]*X[j];  
			}  
			Y[i]=(B[i]-tem)/A[i][i];  
			cout<<left<<setw(8)<<Y[i]<<" ";  
		}  
		cout<<endl;  
		k++;  
		if(k>100){  
			cout<<"迭代失败！（可能是函数不收敛）"<<endl;  
			return ;  
		}  
		
		for(int a=0;a<n;a++){  
			D[a]=X[a]-Y[a];  
		}  
	}while( MaxOfList(D)>0.00001 || MaxOfList(D)<-0.00001);  
	
	return ;  
}  

int main(){  

	int n;  
	cout<<"请输入方程组未知数的个数n：";  
	cin>>n;  
	cout<<endl;  

	vector<vector<double> >A(n,vector<double>(n,0));  
	vector<double>B(n,0);  
	
	cout<<"请输入方程组的系数矩阵："<<endl;  
	for(int i=0;i<n;i++){  
		for(int j=0;j<n;j++){  
			cin>>A[i][j];  
		}  
	}  
	cout<<endl;  
	
	cout<<"请输入方程组的值向量："<<endl;  
	for(int k=0;k<n;k++){  
		cin>>B[k];  
	}  
	cout<<endl;  
	
	cout<<"您输入的方程组为："<<endl;  
	for(int a=0;a<n;a++){  
		for(int b=0;b<n;b++){  
			cout<<A[a][b]<<" ";  
		}  
		cout<<"    "<<B[a]<<endl;  
	}  
	cout<<endl;  
	cout<<"由雅可比迭代公式求的方程组的解为："<<endl;  
	Jacobi(A,B,n);  
	
	//getch();
	system("pause");
	return 0;  
}

例1. 用jacobi迭代法解线性方程组

$\begin{pmatrix} 4 & 3 & 0 \\ 3 & 4 & -1 \\ 0 & -1 & 4 \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \end{pmatrix} = \begin{pmatrix} 24 \\ 40 \\ -24 \\ \end{pmatrix}$

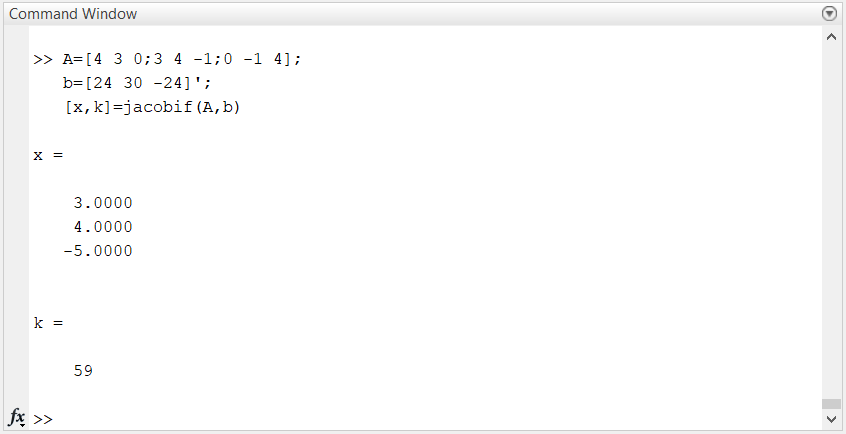
使用MATLAB（Jacobi迭代法分量形式）解决该问题

在MATLAB中输入：
1
2
3
A=[4 3 0;3 4 -1;0 -1 4];
b=[24 30 -24]';
[x,k]=jacobif(A,b)
得到：
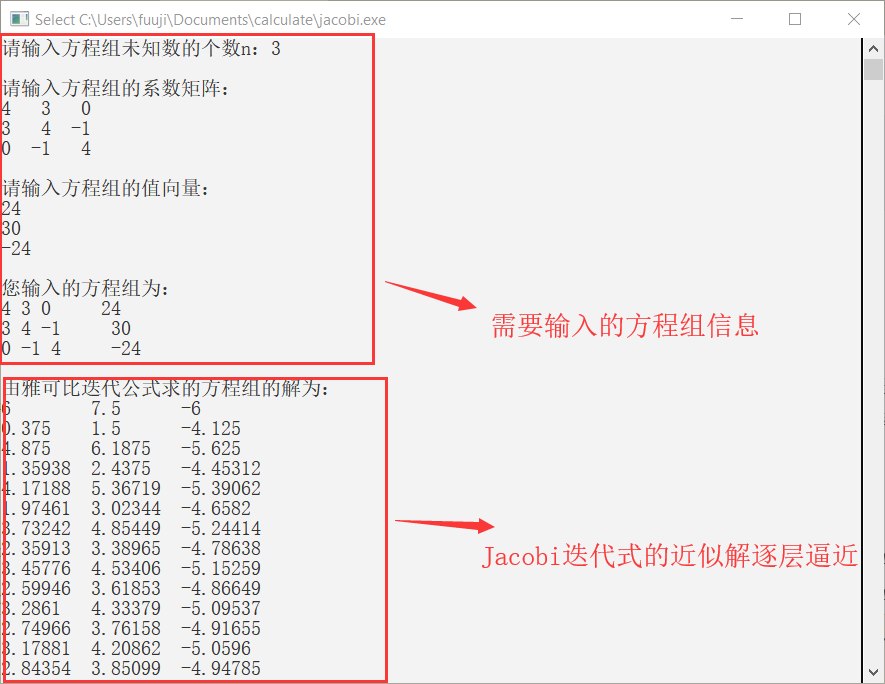
使用c++解决该问题

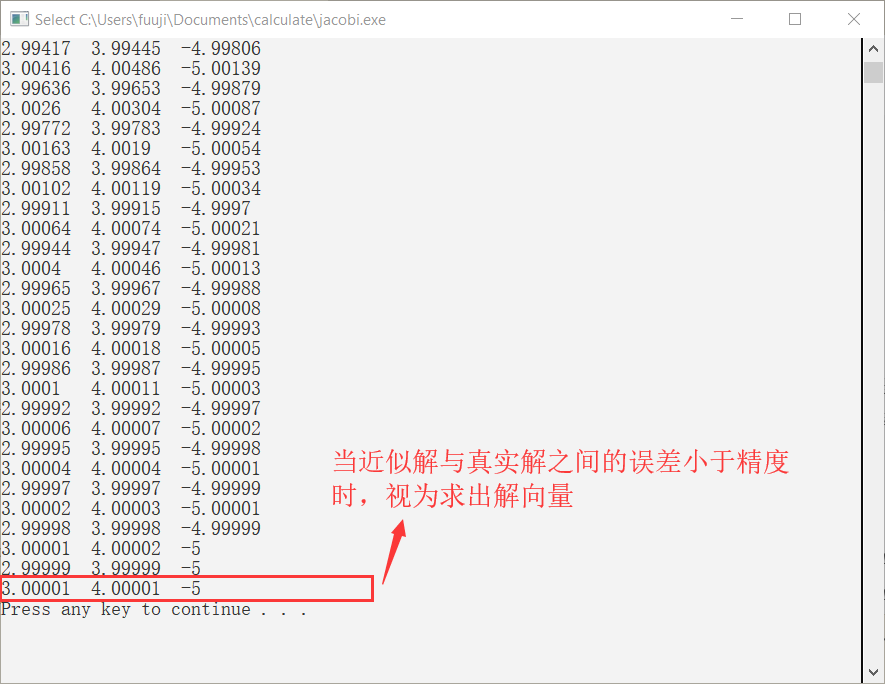
1.3 Gauss-Seidel迭代法以及算法实现

Gauss-Seidel迭代法就是对Jacobi迭代法的一种算法上的优化，让第$i$行的方程都能用上前$i-1$行得出的结果。以$1$和$2$两式对比，更容易看出Gauss-Seidel迭代法的改动优化。

Jacobi迭代法的分量形式
$\begin{cases} x_1^{(k+1)}=\frac{1}{a_{11}}(b_1&-&a_{12}x_2^{(k)}&-&a_{13}x_3^{(k)}&-&\cdots&-&a_{1n}x_n^{(k)})&\\ x_2^{(k+1)}=\frac{1}{a_{22}}(b_2&-&a_{21}x_1^{(k)}&-&a_{23}x_3^{(k)}&-&\cdots&-&a_{2n}x_n^{(k)})&\\ &&&&\vdots\\ x_n^{(k+1)}=\frac{1}{a_{nn}}(b_n&-&a_{n1}x_1^{(k)}&-&a_{n2}x_2^{(k)}&-&\cdots&-&a_{n,n-1}x_{n-1}^{(k)})&\\ \end{cases}$
即（1.10）
$x_i^{(k+1)} = \frac{b_i - \sum_{j=1,j \neq i}^n a_{ij}x_j^{(k)}}{a_{ii}}, \quad i = 1,2,\cdots,n;k = 0,1,2,\cdots.$

Gauss-Seidel迭代法的分量形式
$\begin{cases} x_1^{(k+1)}=\frac{1}{a_{11}}(b_1&-&a_{12}x_2^{(k)}&-&a_{13}x_3^{(k)}&-&\cdots&-&a_{1n}x_n^{(k)})&\\ x_2^{(k+1)}=\frac{1}{a_{22}}(b_2&-&a_{21}x_1^{(k+1)}&-&a_{23}x_3^{(k)}&-&\cdots&-&a_{2n}x_n^{(k)})&\\ &&&&\vdots\\ x_n^{(k+1)}=\frac{1}{a_{nn}}(b_n&-&a_{n1}x_1^{(k+1)}&-&a_{n2}x_2^{(k+1)}&-&\cdots&-&a_{n,n-1}x_{n-1}^{(k+1)})&\\ \end{cases}$
即（1.10）
$x_i^{(k+1)} = -\frac{1}{a_{ii}}\sum_{j=1}^{i-1}a_{ij}x_{j}^{k+1}-\frac{1}{a_{ii}}\sum_{j=i+1}^{n}a_{ij}x_{j}^{k}+\frac{1}{a_{ii}}b_i, \quad (i = 2,3,\cdots,n-1)$

Gauss-Seidel迭代法的MATLAB实现（矩阵形式）

%高斯-赛德尔迭代法，计算线性方程组的解
function [x,k] = Gauss_Seidel_interation(A,b,x0,tol)
% tol为输入误差容限，x0为迭代初始值

% 默认最多迭代300次，超出300次会给出警示
max1 = 300;

%%  diag(diag(X))
%%  取出X矩阵的对角元，然后构建一个以X对角元为对角的对角矩阵。
D = diag(diag(A));

%求A的下三角矩阵,对角线元素为0，再每个矩阵元素取负号
L = -tril(A,-1);

%求A的上三角矩阵，对角线元素为0，再每个矩阵元素取负号
U = -triu(A,1);

% \表示对(D-L)求逆
G = (D-L)\U;
f = (D-L)\b;
x = G*x0+f;
k = 1;

while norm(x-x0)>=tol
	x0 = x;
	x = G*x0+f;
	k = k+1;
	if (k>=max1)
		disp('迭代次数超过',max1,'次，方程组可能不收敛');
	%% 在MATLAB中遇到return的意思就是结束整个函数的执行，
	%% break是仅仅跳出循环体
		return;
	end
	
	%该命令的作用是显示每一步的迭代结果,注意x是列向量，’表示转置的意思，所以要加’
	[k,x']
end

Gauss-Seidel迭代法的C++实现

using namespace std;   
void  Gauss_Seidel(vector<vector<double> > A,vector<double> B,int n)  
{  
	double X[n]={0,0,0,};    
	for (int k=0;k<1000;k++)    
	{    
	for(int i=0;i<n;i++)    
	{    
	double sum=0;    
	for(int j=0;j<n;j++)    
	{    
		if(j==i) continue; //跳过aii  
		sum+=A[i][j]*X[j];    
	}    
	X[i]=(B[i]-sum)/A[i][i];  ///计算完新的x[i],旧的x[i]会被自然冲掉  
	}    
	}    
	for (int i=0;i<n;i++)    
		cout<<"x"<<i+1<<" = "<<X[i]<<'\n';    
		cout<<endl;    
}
int main()  
{  
	int n;  
	cout<<"请输入方程组未知数的个数n：";  
	cin>>n;  
	cout<<endl;  
	
	vector<vector<double> >A(n,vector<double>(n,0));  
	vector<double>B(n,0);  
		
	cout<<"请输入方程组的系数矩阵："<<endl;  
	for(int i=0;i<n;i++){  
		for(int j=0;j<n;j++){  
			cin>>A[i][j];  
		}  
	}  
	cout<<endl;  
		
	cout<<"请输入方程组的值向量："<<endl;  
	for(int k=0;k<n;k++){  
		cin>>B[k];  
	}  
	cout<<endl;  
		
	cout<<"您输入的方程组为："<<endl;  
	for(int a=0;a<n;a++){  
		for(int b=0;b<n;b++){  
			cout<<A[a][b]<<" ";  
		}  
		cout<<" = "<<B[a]<<endl;  
	}  
	cout<<endl;  
	cout<<"由雅可比迭代公式求的方程组的解为："<<endl;  
	Gauss_Seidel(A,B,n);  
	
	system("pause");
	return 0;
}

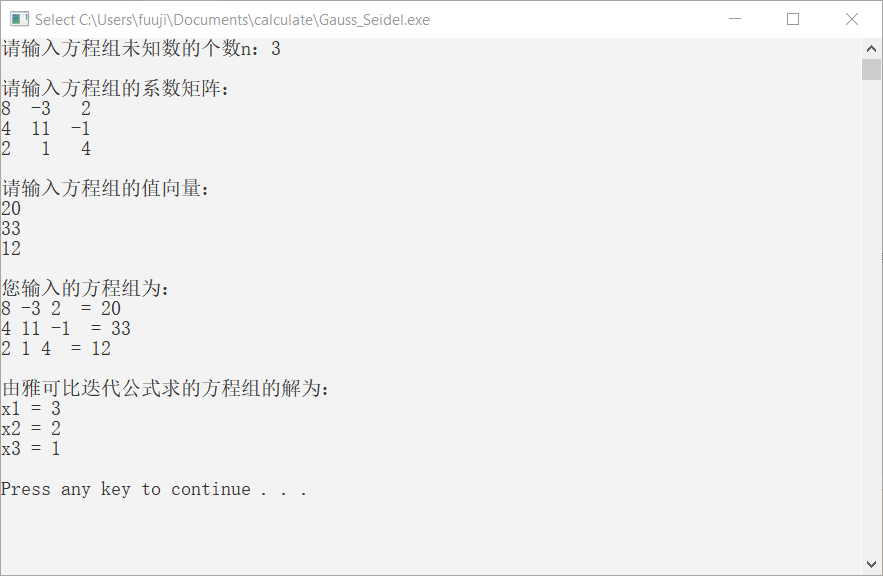
例2. 用 Gauss-Seidel迭代法解线性方程组

$\begin{pmatrix} 8 & -3 & 2 \\ 4 & 11 & -1 \\ 2 & 1 & 4 \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ \end{pmatrix} = \begin{pmatrix} 20 \\ 33 \\ 12 \\ \end{pmatrix}$

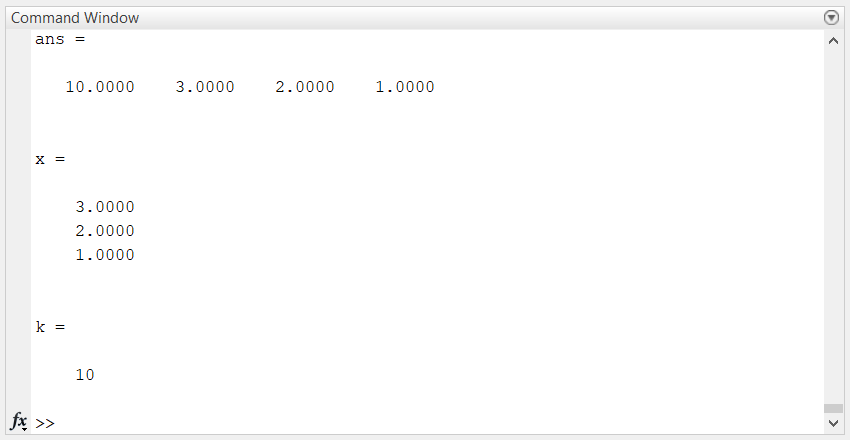
使用matlab（Gauss-Seidel迭代法矩阵形式）解决该问题

在matlab中输入：

 1
2
3
4
A = [8,-3,2;4,11,-1;2,1,4];
b = [20,33,12]';
x0 = [0,0,0]';
[x,k] = Gauss_Seidel(A,b,x0,1e-7)

得到：

使用c++解决该问题

2. 迭代法在非线性方程组数值解法中的运用

主要介绍牛顿迭代法（Newton-Raphson method）的实现和运用。

2.1 牛顿迭代法

牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。

定义

设$r$是$f(x)=0$的根，选取$x0$作为$r$的初始近似值，过点$(x_0,f(x_0))$做曲线$y=f(x)$的切线$L$，$L$的方程为$y=f(x_0)+f’(x_0)(x-x_0)$，求出$L$与$x$轴交点的横坐标$x_1=x_0-\frac{f(x_0)}{f’(x_0)}$，称$x_1$为$r$的一次近似值。过点$(x_1,f(x_1))$做曲线$y=f(x)$的切线，并求该切线与x轴交点的横坐标$x_2=x1-\frac{f(x_1)}{f’(x_1)}$，称$x_2$为$r$的二次近似值。重复以上过程，得r的近似值序列，其中，$x{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}$称为$r$的$n+1$次近似值，上式称为牛顿迭代公式。
牛顿法求解非线性方程

用牛顿迭代法解非线性方程，是把非线性方程$f(x)=0$线性化的一种近似方法。把$f(x)$在点$x0$的某邻域内展开成泰勒级数$f(x)=f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0)(x-x_0)^2}{2!}+ \cdots + \frac{f^{(n)}(x-x_0)^n}{n!}+R_n(x)$，取其线性部分（即泰勒展开的前两项），并令其等于0，即$f(x_0)+f’(x_0)(x-x0)=0$，以此作为非线性方程$f(x)=0$的近似方程，若$f’(x_0)\neq 0$，则其解为$x_1=x_0-\frac{f(x_0)}{f’(x_0)}$，这样，得到牛顿迭代法的一个迭代关系式：$x{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}$。

牛顿法的Matlab实现

% fuujiro
% 2018/6/15
% 迭代参数
x0 = -100; % 初始值
err0 = inf; % 误差初始设为inf
iter = 0;% 迭代次数
errMax = 1e-3; % 最大容许误差
iterMax = 100; % 最大迭代次数

% 迭代过程
x(iter+1) = x0;
while err0>errMax 
	% 迭代终止条件1：达到最大迭代次数
	if iter == iterMax
		disp('达到最大迭代次数！');
		break;
	end
	% Newton迭代过程
	iter = iter+1;
	[~,dy,d2y] = func1(x(iter));
	x(iter+1) = x(iter)-dy/d2y;
	% 迭代终止条件2：找到满足精度要求的解
	if abs(x(iter+1)-x(iter))<errMax
		disp('找到满足精度要求的解！')
		disp(['x = ',num2str(x(iter+1))]);
		disp(['迭代次数为',num2str(iter-1)]);
		break;
	end
end

% 迭代结果展示
plot(x)
xlabel('t');ylabel('x')

牛顿迭代法的C++实现

double func(double x) //函数
{
	return x*x*x*x-3*x*x*x+1.5*x*x-4.0;
}
double func1(double x) //导函数
{
	return 4*x*x*x-9*x*x+3*x;
}
int Newton(double *x,double precision,int maxcyc)      //maxcyc  迭代次数
{
	double x1,x0;
	int k;
	x0=*x;
	for(k=0;k<maxcyc;k++)
	{
		if(func1(x0)==0.0)//若通过初值，函数返回值为0
		{
			printf("迭代过程中导数为0!\n");
			return 0;
		}
		x1=x0-func(x0)/func1(x0);//进行牛顿迭代计算
		if(fabs(x1-x0)<precision || fabs(func(x1))<precision) //达到结束条件
		{
			*x=x1; //返回结果
			return 1;
		}
		else //未达到结束条件
		{
			x0=x1; //准备下一次迭代
		}
	}
	printf("迭代次数超过预期！\n"); //迭代次数达到，仍没有达到精度
	return 0;
}

int main()
{
	double x,precision;
	int maxcyc;
	printf("输入初始迭代值x0:");
	scanf("%lf",&x);
	printf("输入最大迭代次数：");
	scanf("%d",&maxcyc);
	printf("迭代要求的精度：");
	scanf("%lf",&precision);
	if(Newton(&x,precision,maxcyc)==1) //若函数返回值为1
	{
		printf("该值附近的根为：%lf\n",x);
	}
	else //若函数返回值为0
	{
		printf("迭代失败！\n");
	}
	system("pause");
	return 0;
}

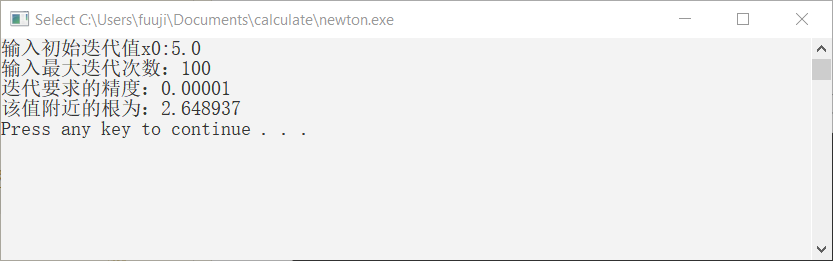
例3：
运行上方的C++代码，计算当初值取$5$时，求根。

结果：

3. 迭代法在实际生活中的运用

在课程之外，我自身也参加了大学生创新创业项目计划，研究课题是机器人手臂视觉标定。简单阐述研究内容是，由于现阶段机器人的视觉标定算法有很多不同的方向和侧重，也有各自的不足，比如标定速度快慢，视觉信息处理速度，算法的时间空间复杂度等等。这些研究者提出的算法都很有创新性，但也会有某些方向的不足。

而我的研究方向，就是尽可能提高视觉标定的准确度，在准确度达标的情况下再尽可能优化标定速度。在前期，我使用的标定算法正巧就是数值计算方法中的牛顿迭代法，因为牛顿法的实现简单且普遍，标定结果也不差。

可能文字难以描述标定过程，放上前期答辩的材料帮助理解。

标定过程
编写代码处理双目深度相机Kinect采集到的数据
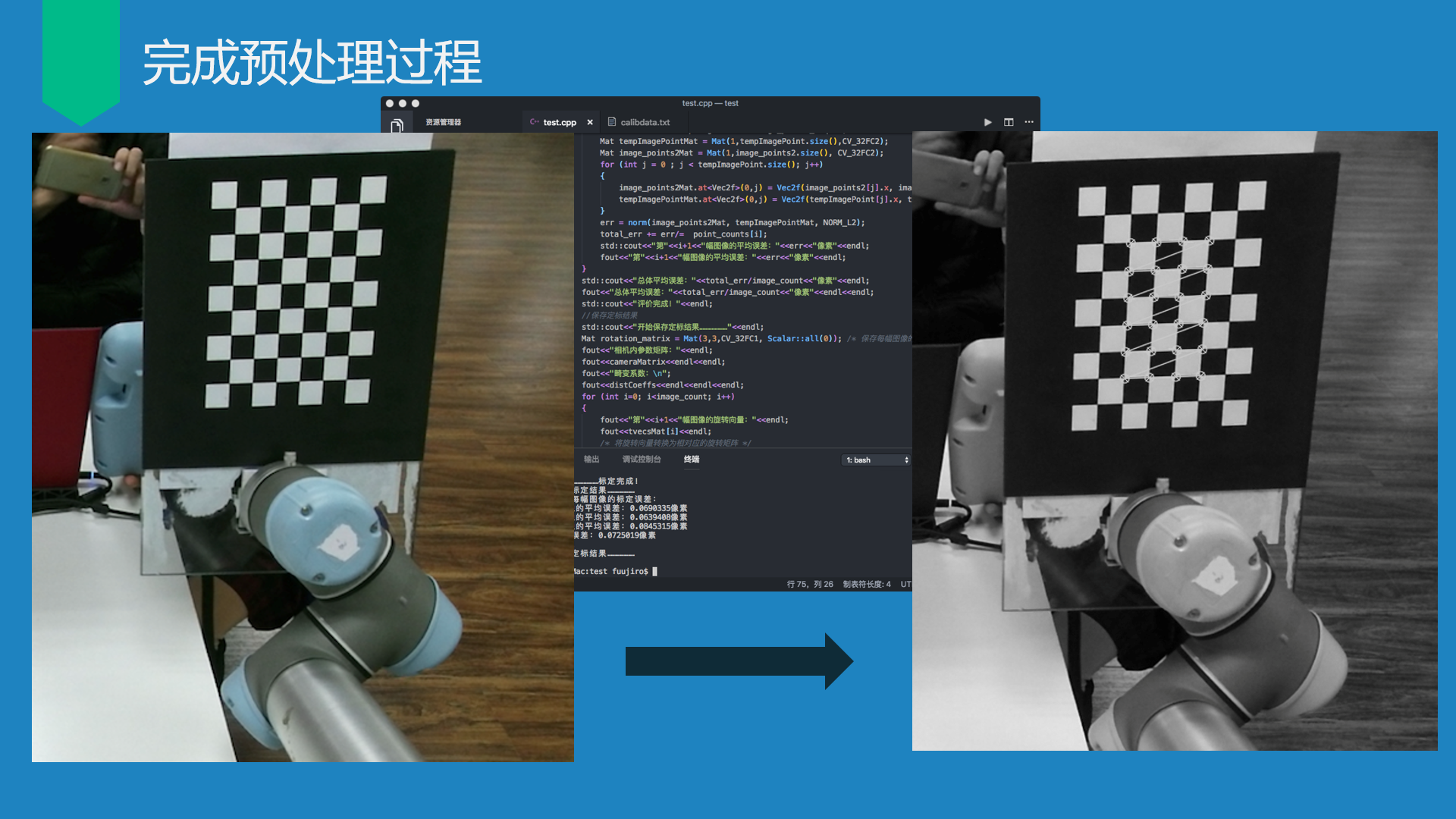
处理完数据后，在原始图像进行黑白格标定
逐步进行迭代法优化，处理结果从左图逐渐优化成右图

简而言之，迭代法在这次大学生创新项目的应用十分成功，我也顺利地通过了前期答辩，拿到了国家级大创项目的评级。

4. 课程感悟

随着计算机和计算方法的飞速发展，几乎所有学科都走向定量化和精确化，从而产生了一系列计算性的学科分支，如计算物理、计算化学、计算生物学、计算地质学、计算气象学和计算材料学等，计算数学中的数值计算方法则是解决“计算”问题的桥梁和工具。

我已经深深地体会到了，计算能力是计算工具和计算方法的效率的乘积，提高计算方法的效率与提高计算机硬件的效率同样重要。科学计算已用到科学技术和社会生活的各个领域中。

数值分析的目的是设计及分析一些计算的方式，可针对一些问题得到近似但够精确的结果。因此在这次的课程设计中我阐述的是迭代法的应用。

迭代法是通过从一个初始估计出发寻找一系列近似解来解决问题的数学过程。和直接法不同，用迭代法求解问题时，其步骤没有固定的次数，而且只能求得问题的近似解，所找到的一系列近似解会收敛到问题的精确解。会利用审敛法来判别所得到的近似解是否会收敛。一般而言，即使使用无限精度算术的计算方式，迭代法也无法在有限次数内得到问题的精确解。

通过课程设计的构思到编写代码实现，我感觉自己对迭代法的理解愈来愈深，深感数学工具与计算数学发展相辅相成。非常感谢孙焘老师对于数值计算方法这门课的付出，希望自己能够踏实地在学习的大路上慢慢走下去。

更新于：2020年9月13日

课程设计

Math

使用KNN算法实现二值化数字和验证码的智能识别

摘要 KNN(K Nearest Neighbor)算法是采用测量不同特征值之间的距离方法进行分类，也就是说对于每个样本数据，需要和训练集中的所有数据进行欧氏距离计算。KNN算法也是机器学习（M...

NJU-计算机系统基础笔记

前言准备自学csapp了，怕听不懂课。知乎说NJU的袁春华老师讲的计算机系统基础特别好，所以准备先学这个好了。 1. 第一章1.1 理解计算机系统抽象层，从上至下依次是：应用（问题），算法，编...